Indice dei contenuti
La maggior parte delle strutture vibrano: durante il normale funzionamento, qualsiasi macchina, veicolo o struttura è sottoposto a delle forze dinamiche che causano delle vibrazioni. In tutti questi casi la risposta strutturale deve essere quantificata, in modo da poterne verificare le implicazioni su fattori quali le prestazioni e la fatica.
Spesso queste vibrazioni devono essere studiate in quanto creano un problema immediato, oppure perché la struttura deve rispondere a delle norme di costruzione o di collaudo. Usando le tecniche di analisi ad elementi finiti, che condividono le basi matematiche con l’analisi del segnale e le misure accelerometriche sperimentali, è possibile determinare la vibrazione della struttura ed eseguire un’analisi in frequenza.
L’analisi modale è uno strumento efficiente per la descrizione, la comprensione e la riduzione a modello del comportamento strutturale e costituisce un mezzo eccellente per acquisire una solida conoscenza della dinamica delle strutture.
Il rumore e le vibrazioni nell’ambiente o nelle industrie sono causati da processi particolari, nei quali delle forze dinamiche, ovvero che variano nel tempo, eccitano una struttura.
Vibrazioni e rumore (definibile come un suono sgradevole) sono strettamente correlati. Il rumore è l’energia vibrazionale trasformata in variazioni di pressione dell’aria che vengono captate dall’orecchio.
Gli effetti del rumore e delle vibrazioni vanno dal semplice disturbo, alla fatica dei materiali e al ridotto comfort, fino alla nocività e al pericolo. Il loro effetto sul corpo umano, sui macchinari, su veicoli o edifici può comportare l’usura, la riduzione delle prestazioni, funzionamento errato o danni irreversibili.
Che cosa è la risonanza?
La maggior parte dei problemi vibrazionali e di rumore sono legati al fenomeno della risonanza. Nel filmato ho riportato il caso del celebre Tacoma Narrow Bridge, famoso per essere collassato a causa dei carichi dinamici del vento, che eccitavano uno dei modi propri della struttura.
Se vuoi vedere il filmato completo, puoi trovarlo a questo link.
Per farla molto-molto semplice, alla frequenza di risonanza le oscillazioni del sistema trasformano alternativamente l’energia cinetica in energia elastica e viceversa. Se eccito la struttura alla frequenza di risonanza, basta una forza di intensità molto piccola per indurre una oscillazione con ampiezza molto elevata.
Chi è responsabile delle vibrazioni?
Se il livello delle vibrazioni o del rumore supera un determinato limite, chi è responsabile del problema?
In ogni situazione possibile esistono sempre tre fattori:
- La Sorgente, ovvero dove si generano le forze dinamiche.
- Il Percorso, come l’energia viene trasmessa.
- Il Ricevitore, dove viene percepito il rumore/vibrazione.
Ciascuno di questi fattori può contenere la causa del problema e può essere esaminato per trovare la soluzione ottimale corrispondente.
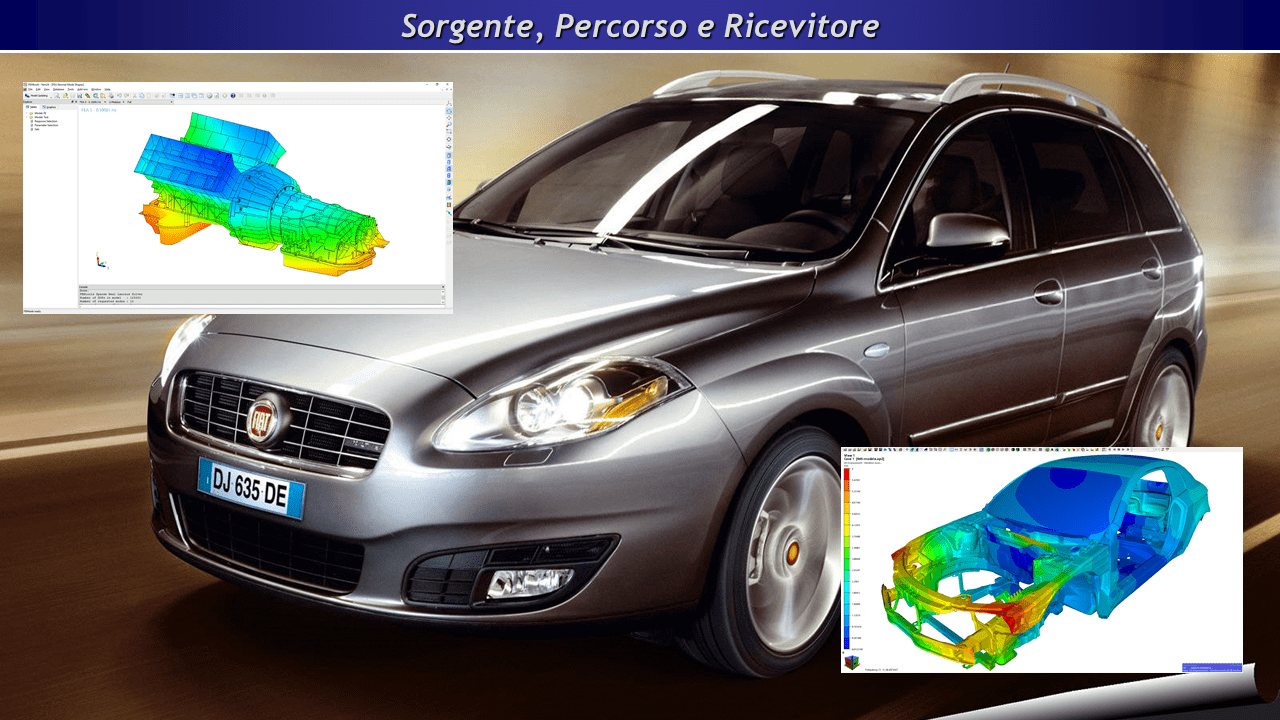
Analisi Modale – Sorgente, Percorso e Ricevitore nel caso di un’autovettura
Prendiamo ad esempio un automobilista che sente che il livello sonoro emesso dalla sua vettura è troppo alto. In questo caso la sorgente è la trasmissione dell’auto, il percorso è il corpo della vettura, il ricevitore è l’orecchio dell’automobilista.
Escludendo che il problema sia l’orecchio dell’automobilista, il responsabile è da identificare tra la trasmissione e il corpo dell’autovettura. Il progettista del telaio e il progettista della trasmissione possono sostenere che le componenti progettate da loro si comportano in modo soddisfacente, se prese singolarmente. Rimane però il fatto che l’interazione tra le due componenti causa un problema serio.
Senza volersi addentrare troppo nei problemi automobilistici, la modellazione ad elementi finiti permette di determinare con un ottimo livello di accuratezza il comportamento dinamico del sistema costituito da vettura e trasmissione, individuando la causa delle vibrazioni e fornendo strumenti analitici per proporre una soluzione.
La simulazione è inoltre in grado di produrre il solito tipo di risultato che si ottiene dalle misure sperimentali. Questo permette da una parte la correlazione tra calcolo e misure per creare modelli accurati, dall’altra (una volta che ho creato un modello predittivo) posso usare il metodo degli elementi finiti per eseguire un virtual test del prodotto, al fine di individuare e risolvere i problemi di vibrazione prima ancora di realizzare il prototipo.
Rappresentazione delle vibrazioni
Quali strutture presentano un comportamento modale? La risposta è semplice: tutte le strutture presentano un comportamento modale. Il comportamento modale dipende da come sono realizzate le strutture, in particolare (come vedremo tra poco), dipende dalla distribuzione di massa e di rigidezza della struttura.
L’analisi modale si basa sul presupposto che il comportamento una struttura complessa costituita da un numero consistente di gradi di libertà (come ad esempio un modello ad elementi finiti dettagliato) possa essere rappresentato adeguatamente attraverso una combinazione lineare di sistemi a un singolo grado di libertà.
Cominciamo ora dando un’idea di come la risposta strutturale possa essere rappresentata in domini diversi. Grazie a questo saremo in grado di vedere come la descrizione modale si collega alle descrizioni nel dominio spaziale, del tempo e della frequenza.
Esempio: la campana
Come esempio prendiamo la risposta di una campana, che è una struttura che presenta uno smorzamento molto basso. Quando una campana viene colpita, questa produce una risposta acustica contenente un numero limitato di toni puri. La risposta vibrazionale associata ha esattamente lo stesso modello e la campana sembra immagazzinare l’energia dall’impatto per dissiparlo poi vibrando a delle frequenze discrete particolari.
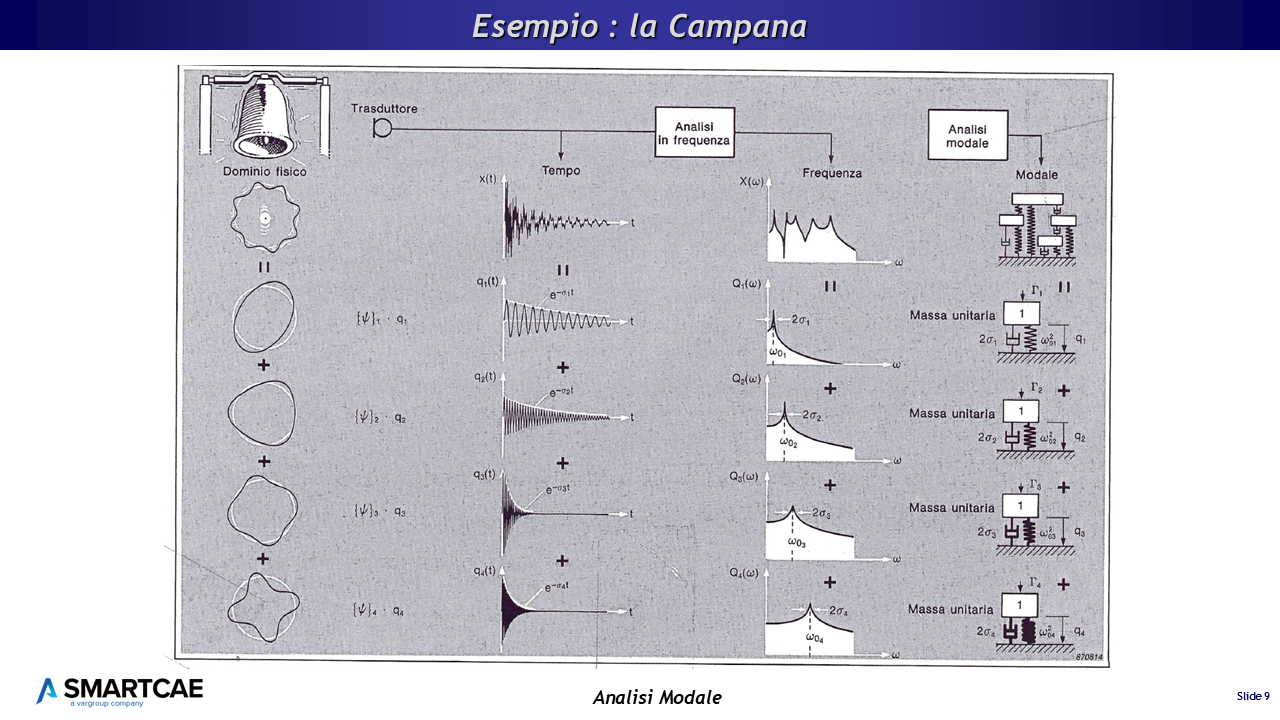
Le varie rappresentazioni della campana nel dominio Spaziale, del Tempo, della Frequenza e Modale
Nello schema in figura, che ho recuperato da un vecchio opuscolo di Bruel&Kjaer sull’analisi modale sperimentale, ciascuna colonna mostra la risposta della campana rappresentata nei diversi domini.
- Nel dominio fisico, la deformazione geometrica complessa della campana può essere rappresentata da un insieme di modelli indipendenti di deformazione, più semplici, che prendono il nome di forme modali.
- Dominio del tempo la risposta vibrazionale (o acustica) della campana è visualizzata sotto forma di un segnale nel tempo che può essere rappresentata da un insieme di sinusoidi che tendono a smorzarsi.
- Nel dominio della frequenza, l’analisi del segnale nel tempo fornisce uno spettro contenente una serie di picchi, rappresentato poi sotto da un insieme di spettri di risposta a singolo grado di libertà.
- Dominio modale si vede la risposta della campana come un modello modale costituito da un insieme di modelli a singolo grado di libertà. Poiché una forma del modo rappresenta il modello del movimento di tutti i punti di una struttura a una frequenza modale, una singola coordinata modale “q” può essere usata per rappresentare l’intera contribuzione di ciascun modo, al movimento.
Se si guarda indietro, a partire dal dominio modale, lungo le linee dell’illustrazione, vediamo come ogni modello a singolo grado di libertà è associato con una frequenza, uno smorzamento, ed una forma del modo. Questi sono i parametri modali.
I parametri modali
Riepilogando in tre righe lo schema precedente:
- Frequenza modale
- Smorzamento modale
- Forma del modo
Costituiscono i parametri modali che, insieme, danno una rappresentazione completa delle caratteristiche dinamiche intrinseche della campana.
Ribadisco un concetto importante: questi parametri sono costanti, e caratteristici della struttura. Nel nostro esempio, le frequenze e la forma dei modi della campana sono sempre gli stessi, sia che la campana suoni o meno.
L’analisi modale è il processo di determinazione dei parametri modali di una struttura, di tutti i modi in una gamma di frequenza di interesse. Lo scopo finale è quello di usare questi parametri per costruire un modello modale della risposta.
A questo punto si devono fare due considerazioni importanti, sotto certe ipotesi:
- Qualsiasi deformazione dinamica forzata di una struttura può essere rappresentata come una somma ponderata delle sue forme modali.
- Ciascun modo può essere rappresentato da un modello a singolo grado di libertà.
Modello a Singolo Grado di Libertà (SGL)
Adesso che abbiamo inquadrato da un punto di vista qualitativo il problema, passiamo e vedere la sua rappresentazione matematica.
Poiché ciascun modo in una risposta strutturale può essere rappresentato da un modello a singolo grado di libertà, è bene esaminare alcuni aspetti della dinamica a singolo grado di libertà. In particolare esamineremo il modo in cui un sistema SGDL può essere modellato nel dominio fisico, del tempo e della frequenza. Questi modelli non sono intesi per la rappresentazione delle strutture fisiche, ma ci servono come strumenti di interpretazione del comportamento dinamico (vincolati da un insieme di ipotesi e condizioni limite).

Analisi Modale – Modello a Singolo Grado di Libertà (SGDL)
Un modello analitico può essere ottenuto nel dominio fisico. La figura illustra il classico sistema a 1 grado di libertà che studiamo nei corsi di meccanica delle vibrazioni, costituito da una inerzia (m), una molla lineare (k) e uno smorzamento viscoso lineare (c). La massa è vincolata a traslare lungo una direzione sola (x), vale a dire che abbiamo un singolo grado di libertà.
Un modello matematico nel dominio del tempo può essere derivato applicando la seconda legge di Newton al modello analitico. Uguagliando le forze interne (inerzia, smorzamento ed elasticità) alle forze esterne (eccitazione) si ricava l’equazione riportata in figura, che è un equazione differenziale del secondo ordine.
Facciamo adesso delle considerazioni.
Al momento non stiamo ancora cercando la risposta del sistema sotto l’azione delle forzanti, ma le caratteristiche intrinseche del sistema… quindi non stiamo applicando una forzante, possiamo eliminare questo termine.
Ipotizziamo anche che lo smorzamento sia basso, cosa che nelle strutture metalliche è verificato nella maggior parte dei casi… quindi eliminiamo questo termine.
Facciamo anche una ipotesi sulla legge di moto, ipotizzando il nostro grado di libertà oscilli con moto sinusoidale. Questo lo facciamo perché esistono altri strumenti matematici, come la trasformata di Fourier, che permettono di trasformare un segnale nel dominio del tempo in una combinazione di sinusoidi.
Quindi l’equazione differenziale del secondo ordine si trasforma in una semplice equazione di secondo grado della quale sappiamo calcolare le radici. Le pulsazioni naturali del sistema crescono al crescere della rigidezza della molla e diminuiscono al crescere della massa. Questa dipendenza della frequenza di risonanza dalla rigidezza e dalla massa è un legame generale (rigidezza al numeratore, massa al denominatore), applicabile in principio a qualsiasi geometria complessa ed è un concetto che qualsiasi progettista dovrebbe avere sempre ben presente.
Modello a gradi di libertà multipli (MGDL)
Nel caso di geometrie complesse, possiamo estendere il ragionamento del modello a singolo grado di libertà a un modello generico a gradi di libertà multipli, cosa che di fatto è un modello agli elementi finiti. Pertanto otteniamo l’equazione riportata in figura.

Analisi Modale – Modello a Gradi di Libertà Multipli (MGDL)
Il problema si riconduce ad un sistema lineare omogeno nelle incognite [omega] e [phi]. Per non annoiarvi ulteriormente con questi aspetti matematici, questa equazione prende il nome di equazione caratteristica del sistema e la soluzione non banale sono i valori di [omega] che prendono il nome di autovalori, cui corrispondono le deformate [phi] che prendono il nome di autovettori.
Gli autovettori possiedono alcune caratteristiche importanti:
- Ortogonalità: sono vettori linearmente indipendenti, ovvero non posso ottenere un autovettore come combinazione lineare degli altri autovettori. Costituiscono quindi una BASE per uno spazio vettoriale (lo spazio modale).
- Normalizzazione: rappresentano solo la forma della deformata, non i valori effettivi della deformata. Per questo motivo occorre utilizzare un criterio per la normalizzazione del vettore. Tipicamente sono proposti due criteri: rispetto alla massa del sistema (da preferire) o imporre l’ampiezza massima pari a 1.
Come si utilizzano i parametri modali?
Una volta che ho calcolato le frequenze e le forme modali cosa ci faccio?
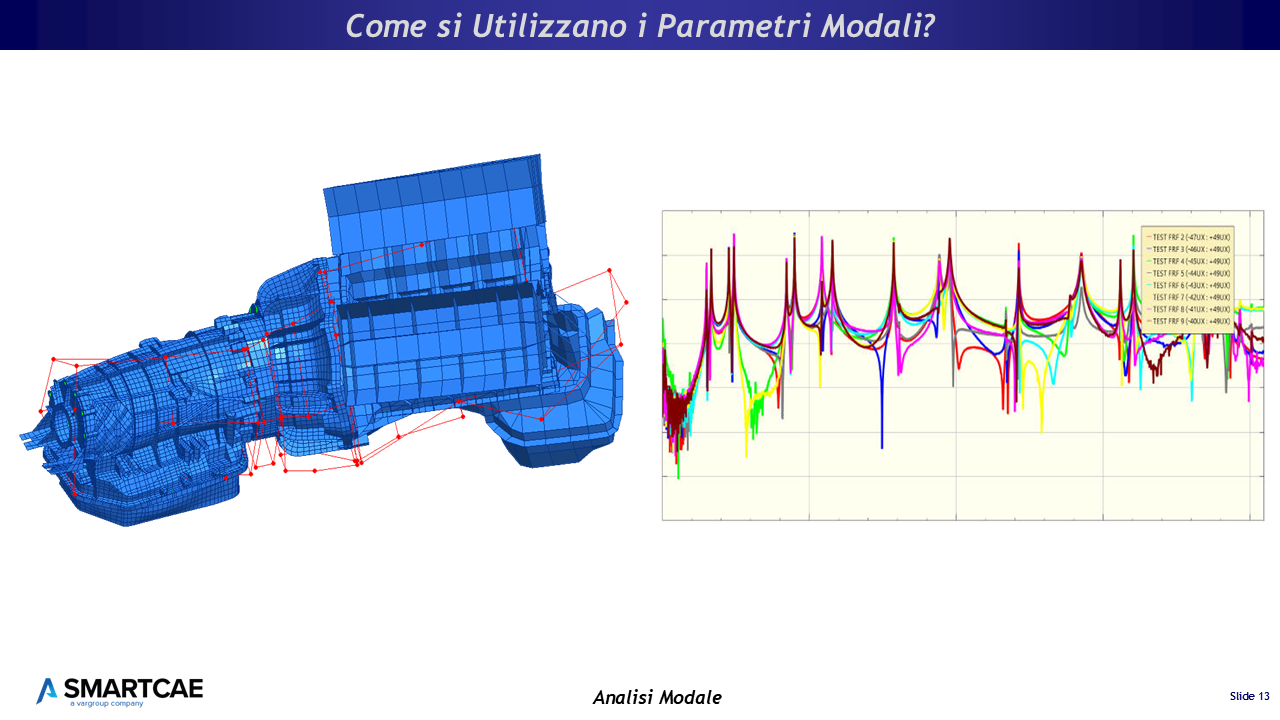
Come si utilizzano i parametri modali
Il primo utilizzo, è quello di interpretarli così come sono, mettendo in relazione il risultato del calcolo con il comportamento meccanico della struttura (modello a sinistra nella figura precedente). In questo caso si valuta se la frequenza di risonanza può generare delle criticità nella struttura nelle condizioni di funzionamento.
Quello che tipicamente viene fatto è assicurarsi che la struttura non presenti frequenze di risonanza nel campo di funzionamento dei dispositivi che possono introdurre una forzante di tipo armonico, e che quindi potrebbero eccitare la struttura.
Il secondo tipo di utilizzo è quello usare la base modale per calcolare la risposta forzata dei sistema (grafico a destra nella figura precedente). Infatti, trasformare le equazioni della dinamica del sistema nello spazio vettoriale costituito dalla base modale vuol dire sostituire un modello da centinaia di migliaia o milioni di gradi di libertà nello spazio fisico con un modello da una manciata di gradi di libertà singoli (tanti quante sono le frequenze di risonanza – e relativi modi – che si considerano rappresentative della risposta dinamica del sistema), per i quali la soluzione numerica è più semplice.
Questa è un’operazione gestita automaticamente dal solutore, l’importante è sapere quali siano le ipotesi alla base di questo approccio, i limiti del metodo e le possibili fonti di errore. Queste cose comunque le vedremo nei prossimi articoli dedicati, appunto, alla risposta in frequenza e alla risposta transitoria.
Domande e risposte
Nel seguito sono indicate alcune domande che mi sono state sottoposte nel corso di seminari e webinar dedicati alla modellazione FEM per l’analisi modale. Ho deciso di riportarle perché in questo post perché potranno esserti di aiuto nel definire la migliore strategia di modellazione FEM per schematizzare il contatto.
La mesh preparata per la stress analysis va bene anche per l’analisi dinamica?
In linea di principio, una mesh realizzata per il calcolo delle sollecitazioni, può andare bene anche per la dinamica. Infatti anche noi, quando possibile, cerchiamo di realizzare un modello unico sul quale eseguire più simulazioni.
La cosa importante da tenere presente è che il calcolo degli autovalori è molto più oneroso di una statica lineare, pertanto tutte le semplificazioni del caso sono lecite: ad esempio l’utilizzo degli shell e dei beam e dei parametri concentrati al posto di una mesh a solidi.
Inoltre siccome ad ogni forma modale corrisponde un set di risultati completo, bisogna fare attenzione ai risultati da chiedere nell’analisi, altrimenti il database dei risultati potrebbe lievitare a dismisura.
A meno che non si desideri effettuare una analisi successiva di risposta in frequenza, conviene includere nei risultati soltanto i displacements e, eventualmente, l’energia di deformazione elastica.
Che cosa è l’analisi modale Free-Free?
Domanda molto interessante, perché mi sono dimenticato di toccare questo argomento in precedenza. Per rispondere prendo la slide con l’equazione caratteristica.
L’equazione caratteristica ammette una soluzione anche se non vado ad introdurre dei vincoli nel sistema. Le frequenze naturali esistono infatti anche per un corpo che è sospeso nell’aria, senza vincoli. In questo caso si parla di parla di sistema free-free.
Quando eseguiamo un calcolo modale senza vincolare il sistema, otterremo 6 autovettori con frequenza molto bassa, praticamente a 0 Hz. Questi autovettori sono le forme di corpo rigido, ovvero sono delle oscillazioni di roto-traslazione di tutto il sistema nello spazio. Dopo le forme di corpo rigido, a frequenze diverse da zero, avremo poi i modi elastici.
L’ampiezza delle deformazioni modali ha significato fisico?
Se la nostra indagine riguarda soltanto l’analisi modale, non devo guardare ai valori dei risultati modali (deformazioni ed energia di deformazione elastica) in termini assoluti ma relativi.
Questo perché l’ampiezza dello spostamento modale (e conseguentemente della strain energy) dipende dal criterio di normalizzazione degli autovettori che è stato utilizzato. La normalizzazione introduce uno fattore di scala arbitrario su tutta la deformata modale.
Ad esempio per NX Nastran il criterio di default è la normalizzazione rispetto alla matrice di massa. Altri solutori come il vecchio Ideas utilizzava di default la normalizzazione unitaria.
Si può tenere conto di urti e contatti nell’analisi modale?
La risposta è NO, nell’analisi modale non si può tenere conto né degli urti né dei contatti tra i corpi.
L’analisi modale, ovvero l’estrazione degli autovalori e degli autovettori, è un calcolo eseguito nell’ipotesi di modello lineare.
Pertanto fenomeni non lineari come urti e contatti devono essere approssimati nel modello con elementi di tipo lineare. Questo vuol dire, ad esempio, che posso incollare le parti tra di loro, ma non posso usare il contatto.
Questo limite accomuna l’analisi modale all’analisi di risposta in frequenza.
Se desidero studiare il comportamento dinamico del sistema, tenendo conto dei fenomeni non lineari quali il contatto o gli urti, l’unica strada è quella di eseguire una analisi transitoria non lineare, quindi nel dominio del tempo.
Che differenza c’è tra matrice di massa coupled e matrice lumped?
Questa è una tecnica di gestione della matrice di massa del sistema da parte del solutore.
La matrice di massa coupled, o completa, è una matrice sparsa variamente popolata che contiene i termini di inerzia. Data una mesh FEM, questa è la rappresentazione più accurata della massa del sistema.
La matrice lumped, usa una semplificazione di sommare nei termini che si trovano sulla diagonale della matrice anche i contributi dell’inerzia che si trovano fuori della diagonale. Questo si traduce in un consistente risparmio di memoria.
Con la potenza di calcolo e la RAM disponibile al giorno d’oggi, secondo me non ha più senso utilizzare la matrice lumped, a meno che non sia prescritto da procedure particolari.
Argomenti collegati
Articoli
- Cosa è l’analisi di risposta in frequenza con gli elementi finiti
- Cosa è l’analisi transitoria con gli elementi finiti
Webinar