Indice dei contenuti
In questo articolo continuo la trattazione dell’analisi dinamica con gli elementi finiti, affrontando il tema della risposta in frequenza.
Nell’articolo precedente che spiega cosa è l’analisi modale con gli elementi finiti, abbiamo visto che l’analisi modale si basa sul presupposto che il comportamento di una struttura complessa costituita da un numero consistente di gradi di libertà (come ad esempio un modello ad elementi finiti dettagliato) possa essere rappresentato adeguatamente attraverso una combinazione lineare di sistemi a un singolo grado di libertà. Nell’esempio della campana, abbiamo introdotto il concetto di dominio fisico, dominio del tempo, dominio della frequenza.
Per risparmiarti di andare a cercare l’articolo, riporto brevemente la figura e le considerazioni che abbiamo fatto.

Le varie rappresentazioni della campana nel dominio Spaziale, del Tempo, della Frequenza e Modale
Quando una campana viene colpita, questa produce una risposta acustica contenente un numero limitato di toni puri. La risposta vibrazionale associata ha esattamente lo stesso comportamento e la campana sembra immagazzinare l’energia dall’impatto per dissiparlo poi vibrando a delle frequenze discrete particolari.
- Nel dominio fisico, la deformazione geometrica complessa della campana può essere rappresentata da un insieme di modelli indipendenti di deformazione, più semplici, che prendono il nome di forme modali. Per un modello FEM, espresso analiticamente con matrici di massa e rigidezza, le forme modali coincidono con gli autovettori dell’equazione caratteristica.
- Per dominio del tempo la risposta vibrazionale (o acustica) della campana è visualizzata sotto forma di un segnale nel tempo che può essere rappresentata da un insieme di sinusoidi che tendono a smorzarsi.
- Nel dominio della frequenza, l’analisi del segnale nel tempo fornisce uno spettro contenente una serie di picchi, rappresentato poi sotto da un insieme di spettri di risposta a singolo grado di libertà.
- Nel dominio modale si vede la risposta della campana come un modello modale costituito da un insieme di modelli a singolo grado di libertà. Poiché una forma del modo rappresenta il modello del movimento di tutti i punti di una struttura a una frequenza modale, una singola coordinata modale “q” può essere usata per rappresentare l’intera contribuzione di ciascun modo, al movimento.
In questo articolo vediamo cosa succede nel passaggio tra le ultime due colonne.
Modello parametrico spaziale
Prendiamo un sistema a singolo grado di liberta, costituito da un modello parametrico caratterizzato da una massa, una rigidezza e uno smorzamento viscoso, come quello illustrato in figura.
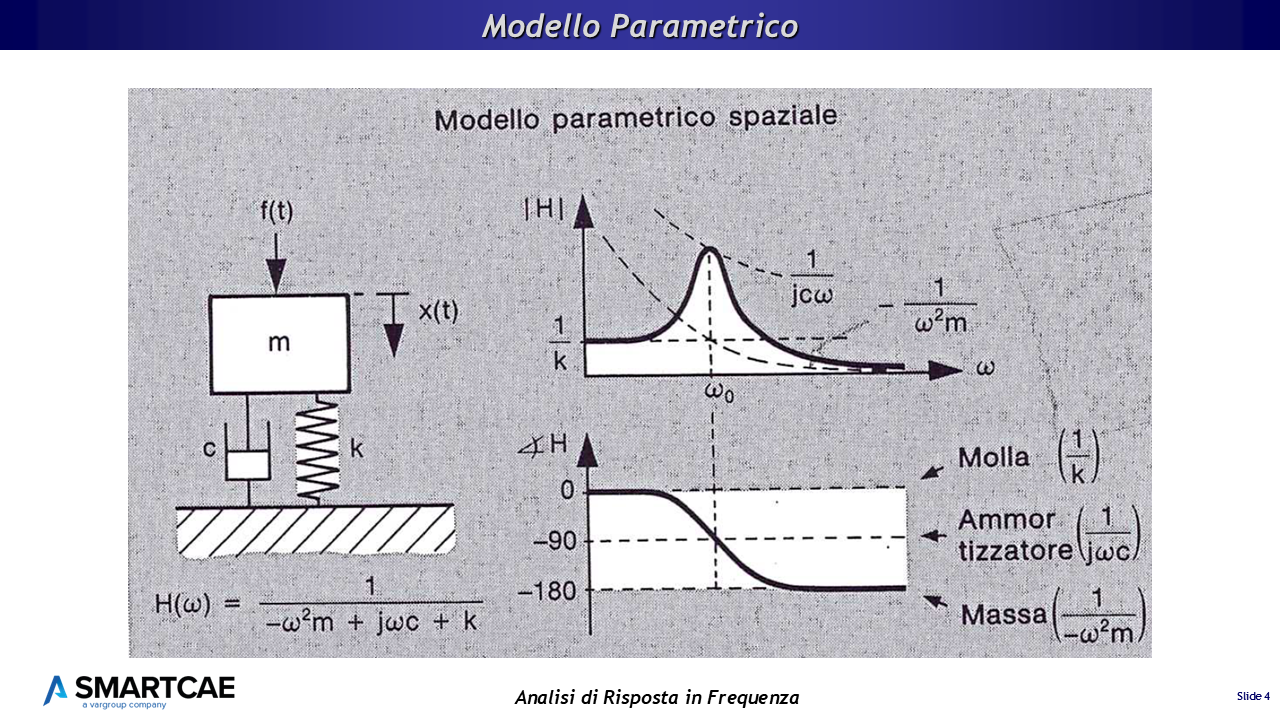
Modello parametrico spaziale
Esaminiamo il suo comportamento quando è sottoposto a una eccitazione sinusoidale e vediamo cosa accade all’ampiezza e alla fase dell’oscillazione al variare della frequenza di eccitazione.
- A frequenza nulla, la deformazione statica è controllata dalla sola rigidezza della molla.
- A bassa frequenza, la risposta è dominata dalla rigidezza ed è in fase con l’eccitazione.
- All’aumentare della frequenza la forza d’inerzia della massa assume un’influenza sempre più importante, finché ad una frequenza particolare (w0 = frequenza naturale non smorzata) i termini elastici e di inerzia si annullano reciprocamente. La risposta è controllata unicamente dallo smorzamento e la cedevolezza diventa alta. Se lo smorzamento fosse nullo, la cedevolezza assumerebbe allora un valore infinito. Alla frequenza w0 la risposta è ritardata di 90° rispetto all’eccitazione.
- A frequenze superiori a w0 il termine di massa prende il controllo ed il sistema progressivamente comincia a comportarsi semplicemente come una massa, la cedevolezza diminuisce e la risposta è ritardata di 180° rispetto all’eccitazione.
Il comportamento in frequenza può essere espresso in maniera analitica attraverso l’equazione H(w) che si vede in figura, che prende il nome di cedevolezza.
Modello FRF
Quello illustrato in figura è un altro modello per rappresentare il comportamento dinamico del sistema generale con più gradi di libertà.

Modello FRF
Si chiama modello FRF, ovvero Funzione di Risposta in Frequenza ed è basato sulla cedevolezza H(w).
Da un punto di vista sperimentale H(w) è il rapporto tra gli spettri di uscita e gli spettri di ingresso, dal punto di vista FEM è il rapporto tra lo spostamento del punto e la forza applicata. In entrambi i casi è una grandezza che varia con la frequenza (w).
Quella che abbiamo chiamato cedevolezza può prendere altri nomi, in base alla grandezza che prendiamo sia come eccitazione che come risposta (spostamento, velocità o accelerazione) oppure dal come è definito il rapporto.
Nella slide ho riportato alcune delle funzioni di risposta in frequenza che si trovano in letteratura.
Passare dall’una all’altra anche se è semplice, non è immediato in quanto l’operazione di derivazione per passare da spostamento a velocità a accelerazione ha l’effetto di moltiplicare per j (quindi cambiano parte reale con parte immaginaria, oppure cambia la fase per vederla dall’altro punto di vista) e per la pulsazione Omega.
Si tratta comunque di operazioni che possono essere effettuate anche con excel.
Alcune considerazioni
Da quanto abbiamo visto in precedenza, la risposta in frequenza di un sistema dinamico coinvolge alcuni concetti che dobbiamo sempre avere presenti.
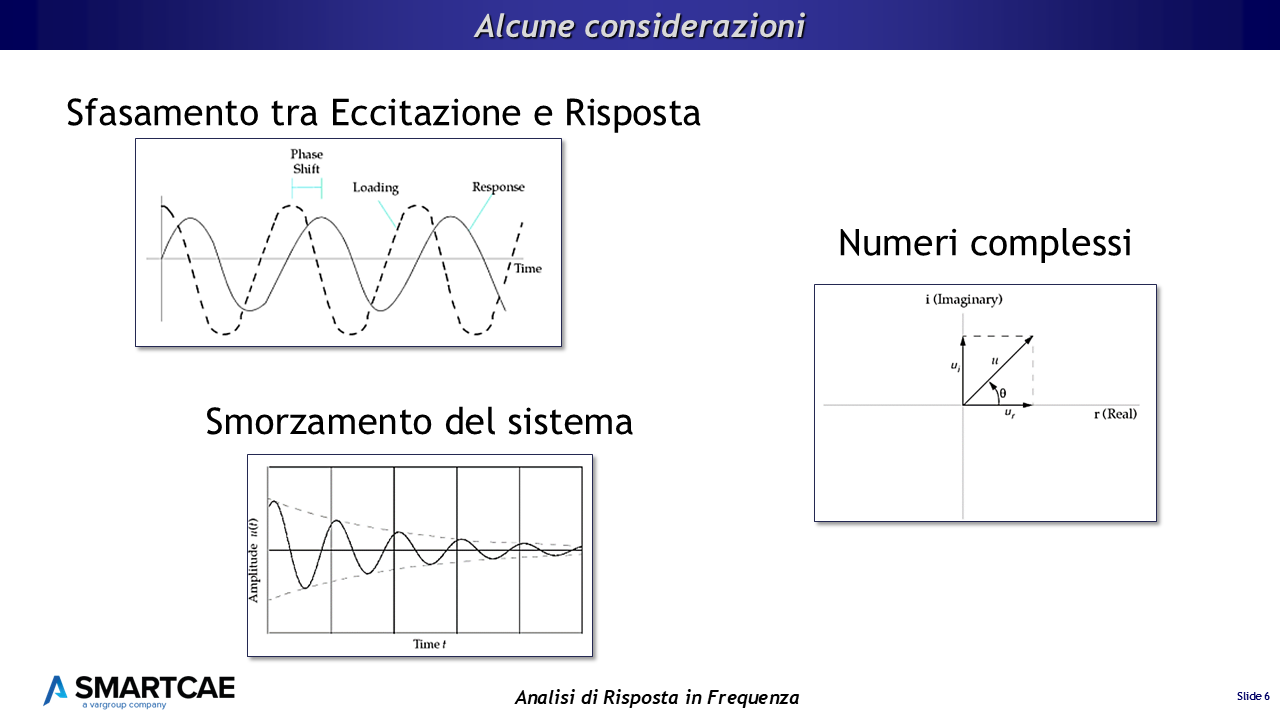
Considerazioni sulla risposta in frequenza
Per prima cosa, dobbiamo aspettarci uno sfasamento, tra l’istante in cui viene applicato il carico massimo e l’istante in cui viene determinata la risposta massima. Questo sfasamento dipende da vari fattori ed è qualcosa che è intrinseco nell’analisi dinamica. Abbiamo visto, ad esempio, che alla risonanza lo sfasamento è 90° e questo può essere di aiuto a interpretare i risultati.
Per gestire la risposta dinamica è quindi necessario rappresentare i risultati nella forma di numeri complessi, con parte reale e parte immaginaria. Questo ci permette di definire con una coppia di valori (ampiezza e fase oppure parte reale e parte immaginaria) la risposta in maniera biunivoca rispetto all’eccitazione.
L’ampiezza della risposta dipende da un parametro, che fino ad ora abbiamo bellamente trascurato, che è lo smorzamento.
Spontaneamente, una struttura che oscilla liberamente senza forzanti esterne, tende a ridurre l’ampiezza dell’oscillazione fino ad arrestarsi. Lo smorzamento è la forza che si oppone all’oscillazione e deve essere considerata nei nostri calcoli. Come vedremo tra breve, è lecito trascurare lo smorzamento nel calcolo delle frequenze di risonanza del sistema, mentre non è possibile trascurarlo per il calcolo della funzione di risposta in frequenza, quindi dobbiamo trovare la maniera di inserirlo nel calcolo.
Purtroppo per noi non solo esistono molti modi per definire lo smorzamento, ma nella realtà esistono anche diversi tipi di smorzamento, e vari modi per inserirlo nel modello agli elementi finiti. Tutto questo aspetto richiede un approfondimento.
Da cosa è generato lo smorzamento?
Lo smorzamento è un’approssimazione matematica utilizzata per rappresentare la dissipazione di energia che si osserva nelle strutture. Lo smorzamento è difficile da modellare accuratamente in quanto è causato da vari meccanismi che includono:
- Gli Effetti Viscosi, ovvero l’energia dissipata per scorrimento viscoso nei fluidi. Questo tipo di fenomeno si manifesta quando nel modello sono presenti pistoni idraulici o pneumatici, ammortizzatori o altri sistemi che utilizzano appunto dei fluidi per il loro funzionamento.
- Attriti esterni, ovvero l’energia viene dissipata per attrito coulombiano quando due corpi scorrono e si sfregano l’uno con l’altro.
- Attriti interni al materiale, quali interazioni tra molecole o grani cristallini o altre strutture elementari del materiale. Questa è una proprietà intrinseca del materiale.
- Effetti non lineari quali la plasticizzazione, apertura e chiusura di gap che portano a urti localizzati.
Come puoi immaginare, è ben difficile riuscire a schematizzare tutti questi fenomeni in un modello FEM, per questo motivo lo smorzamento tipicamente viene approssimato in maniera semplice. Questa semplificazione è anche giustificata dal fatto che, in generale, i valori dello smorzamento sono bassi e non si commette un grosso errore se lo si approssima con una formulazione facile da gestire.
Di fatto, i modelli di smorzamento che vengono utilizzati nei modelli lineari sono sostanzialmente di tre tipi: il modello Viscoso e il modello Strutturale (che hanno una corrispondenza con le proprietà della struttura) e il modello Modale (che è una caratteristica dei modi propri della struttura).
Andiamo a vederli nel dettaglio…
Smorzamento viscoso e smorzamento strutturale
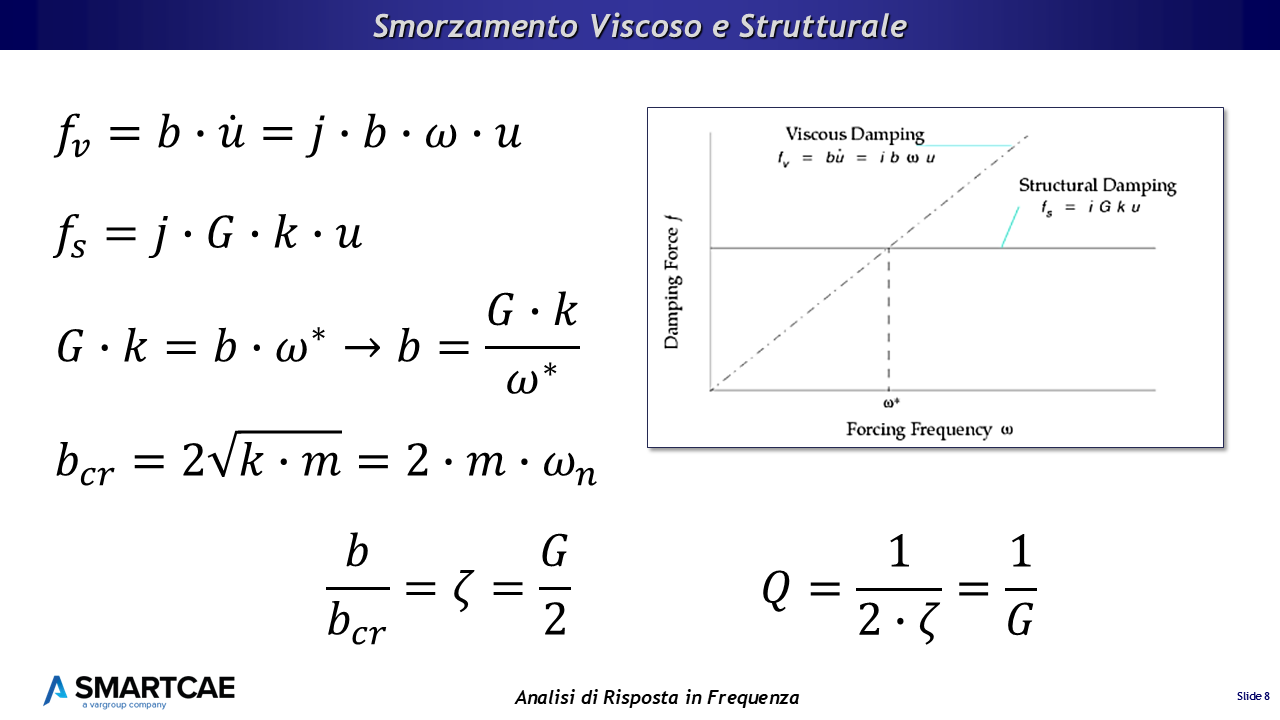
Analisi FRF – Smorzamento viscoso e smorzamento strutturale
Consideriamo sempre il nostro modello a un grado di libertà soggetto a un moto oscillatorio sinusoidale.
La forza di smorzamento viscoso è data dall’attrito viscoso del fluido e pertanto è proporzionale alla velocità dell’oscillazione ed è espressa nella prima equazione, nella quale b è il coefficiente di smorzamento viscoso j omega u è la velocità.
La forza di smorzamento strutturale è invece dovuta a una dissipazione interna al materiale ed è pertanto proporzionale agli spostamenti, come si vede nella seconda equazione, dove:
- G è il coefficiente di smorzamento strutturale;
- K è la rigidezza
- U sono gli spostamenti
“j” che compare in entrambe le equazioni è l’unità immaginaria, ovvero la radice quadrata di meno 1 che corrisponde a uno sfasamento di 90°
Nel caso di una risposta sinusoidale con ampiezza degli spostamenti costante, la forza di smorzamento strutturale è costante e indipendente dalla frequenza di oscillazione, mentre la forza di smorzamento viscoso è proporzionale alla frequenza. Dalla figura si vede che queste due funzioni si intersecano per un valore particolare della frequenza w*, dove queste due forze sono identiche.
Richiamando la definizione di smorzamento critico, si derivano delle equazioni che sono valide alla risonanza, per spostamenti sinusoidali di ampiezza costante:
- Nella prima viene definito [zeta], il rapporto tra lo smorzamento e lo smorzamento critico. Lo smorzamento critico è quel valore di smorzamento per il quale il sistema esegue una sola oscillazione, che si smorza e si completa in un tempo infinito.
- Nella seconda viene definito Q, il fattore di amplificazione dinamica che è inversamente proporzionale all’energia dissipata in un ciclo di vibrazione.
Pertanto, nel modello FEM per la risposta dinamica devo utilizzare almeno uno di questi due modelli di smorzamento assegnando i valori opportuni.
Oltre a questi due modelli, esistono altre forme adimensionali per esprimere lo smorzamento: quality factor, loss factor, decremento logaritmico… una discussione di queste forme va al di là dello scopo di questo articolo.
Smorzamento Modale
Un altro modello di smorzamento che è utilizzato molto spesso è lo smorzamento modale. In questo caso lo smorzamento è applicato ad ogni modo separatamente. Questo modello è la scelta più ovvia quando l’analisi è eseguita nel dominio modale (vedremo tra breve cosa si intende per dominio modale).

Analisi FRF – Smorzamento modale
Lo smorzamento raramente è distribuito uniformemente attraverso la struttura e, di conseguenza, alcuni modi di vibrare possono avere uno smorzamento molto piccolo, e altri uno smorzamento più elevato. Per esempio una struttura può manifestare un modo che coinvolge la vibrazione dei giunti, provocando scorrimenti locali e quindi uno smorzamento elevato. Altri modi, sulla medesima struttura, non coinvolgono i giunti e quindi lo smorzamento è più basso.
Quando si utilizza lo smorzamento modale, ogni modo presenta uno smorzamento Bi che dipende, oltre che dalla pulsazione di oscillazione, anche dalla massa modale e dal coefficiente di smorzamento modale.
Per un modello a singolo grado di libertà lo smorzamento critico è definito come 2 volte la radice del prodotto tra massa e rigidezza.
Con [omega_D] indichiamo la pulsazione naturale smorzata, che differisce da quella del sistema non smorzato.
Ma di quanto differisce?
Nella pratica, la maggior parte delle strutture manifestano uno smorzamento modale compreso tra lo 0% e il 10%… Per le strutture metalliche in acciaio o ghisa, tipicamente si utilizzano valori intorno al 2% o 3%.
Si vede subito che mettendo un valore del 3% in questa equazione, la pulsazione naturale del sistema smorzato coincide praticamente con quella del sistema non-smorzato. Per questo motivo è lecito trascurare lo smorzamento nel calcolo delle frequenze di risonanza della struttura. Questo però non implica che lo smorzamento possa essere trascurato nel calcolo della funzione di risposta in frequenza… tutt’altro!
Abbiamo visto che l’ampiezza dell’oscillazione alla risonanza dipende dallo smorzamento: minore è lo smorzamento, più ampia è l’oscillazione.
Chiusa questa parentesi sullo smorzamento, possiamo parlare del calcolo delle funzioni di risposta in frequenza (FRF).
Calcolo della funzione di risposta in frequenza
Esistono due moetodi per calcolare la risposta in frequenza del sistema con il solutore agli elementi finiti:
- Metodo diretto
- Metodo modale
Andiamo a vederli.
FRF calcolata con il metodo diretto
Adesso che abbiamo definito lo smorzamento, riscriviamo l’equazione del moto di un sistema con molteplici gradi di libertà. Come sappiamo, la formulazione FEM riconduce la descrizione del modello ad una matrice di massa, di rigidezza e di smorzamento del sistema.

Funzione di risposta in frequenza FRF calcolata con il metodo diretto
Applicando la seconda legge di Newton, otteniamo una serie di equazioni del moto, un equazione per ogni grado di libertà del modello.
Nell’ipotesi di eccitazione di tipo sinusoidale e di sistema lineare, è possibile riscrivere la forzante e le risposte utilizzando una notazione compatta.
Questo si traduce nella possibilità di riscrivere l’equazione del moto con i tre termini: forze d’inerzia, forze viscose e forze elastiche che equilibrano istantaneamente le forzanti armoniche.
Risolvere questa equazione è esattamente quello che esegue Nastran quando lanciamo una SOL 108, ovvero il calcolo della risposta dinamica con il metodo diretto.
Prende il nome di metodo diretto in quanto il solutore, per ogni valore di frequenza per cui voglio calcolare la risposta, effettua il prodotto delle matrici di sistema per i termini -w2, +jw e risolve l’equazione per calcolare gli spostamenti u.
Questo si traduce in eseguire molte volte l’assemblaggio e l’inversione della matrice del sistema, con tempi calcolo molto consistenti.
Fortunatamente per la maggior parte delle applicazioni ingegneristiche, è possibile utilizzare un approccio nel quale ci viene in aiuto l’analisi modale, in particolare gli autovettori del sistema.
FRF calcolata con il metodo modale
Ricordando l’articolo sull’analisi modale, gli autovettori del sistema costituiscono una base per uno spazio vettoriale. Utilizziamo proprio questa proprietà per trasformare il problema dallo spazio geometrico allo spazio costituito dalle forme modali.

Funzione di risposta in frequenza FRF calcolata con il metodo modale
Per arrivare al risultato, ipotizziamo di trascurare per un momento lo smorzamento (abbiamo visto prima che è un’ipotesi sensata) e utilizziamo, come prima una forzante di tipo sinusoidale.
Stavolta però facciamo una trasformazione di coordinate: definiamo gli spostamenti attraverso la matrice degli autovettori e le coordinate generalizzate Xi.
Pre-moltiplicando tutti i termini per la matrice degli autovettori trasposta, si ottiene il risultato cercato.
Il primo termine prende il nome di matrice di massa modale, il secondo rigidezza modale e il terzo forzante modale.
Il sistema di equazioni è disaccoppiato e posso calcolare rapidamente la risposta con delle semplici equazioni di modelli a singolo grado di libertà.
Potrei definire lo smorzamento come attributo del modo (si parla infatti di smorzamento modale), mantenendo le equazioni disaccoppiate.
In altri casi i termini di smorzamento, sia viscoso che strutturale, non possono essere approssimati con lo smorzamento modale. In questo caso è necessario calcolare le matrici di smorzamento modali con i termini viscosi che vanno a moltiplicare le velocità e i termini strutturali che vanno a moltiplicare gli spostamenti.
Questo conduce a un sistema con equazioni accoppiate, più complesso da risolvere rispetto al sistema disaccoppiato. Inoltre si approssima lo smorzamento strutturale con uno viscoso equivalente.
Nella pratica il numero di autovettori utilizzato per la trasformazione è tipicamente di ordini di grandezza inferiore rispetto al numero di gradi di libertà del modello, pertanto il tempo di calcolo della FRF con il metodo modale è nettamente inferiore rispetto al metodo diretto.
Complessivamente, considerando anche il calcolo della base modale, rimane comunque il netto vantaggio di riuscire a calcolare la risposta FRF in una frazione del tempo che richiede l’approccio diretto.
Una volta risolto il problema per i gradi di libertà generalizzati [xi], il solutore esegue il prodotto riga per colonna riportato nell’equazione per trasformare i risultati nello spazio geometrico, e visualizzare i risultati in maniera comprensibile per l’utente.
Confronto tra FRF calcolate con il metodo diretto e il metodo modale
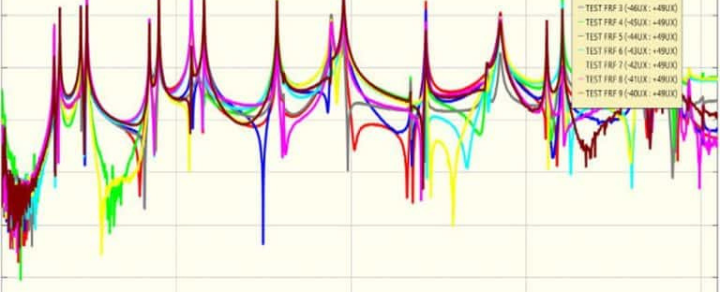
In questo grafico sono riportate tre curve FRF calcolate sul medesimo modello.
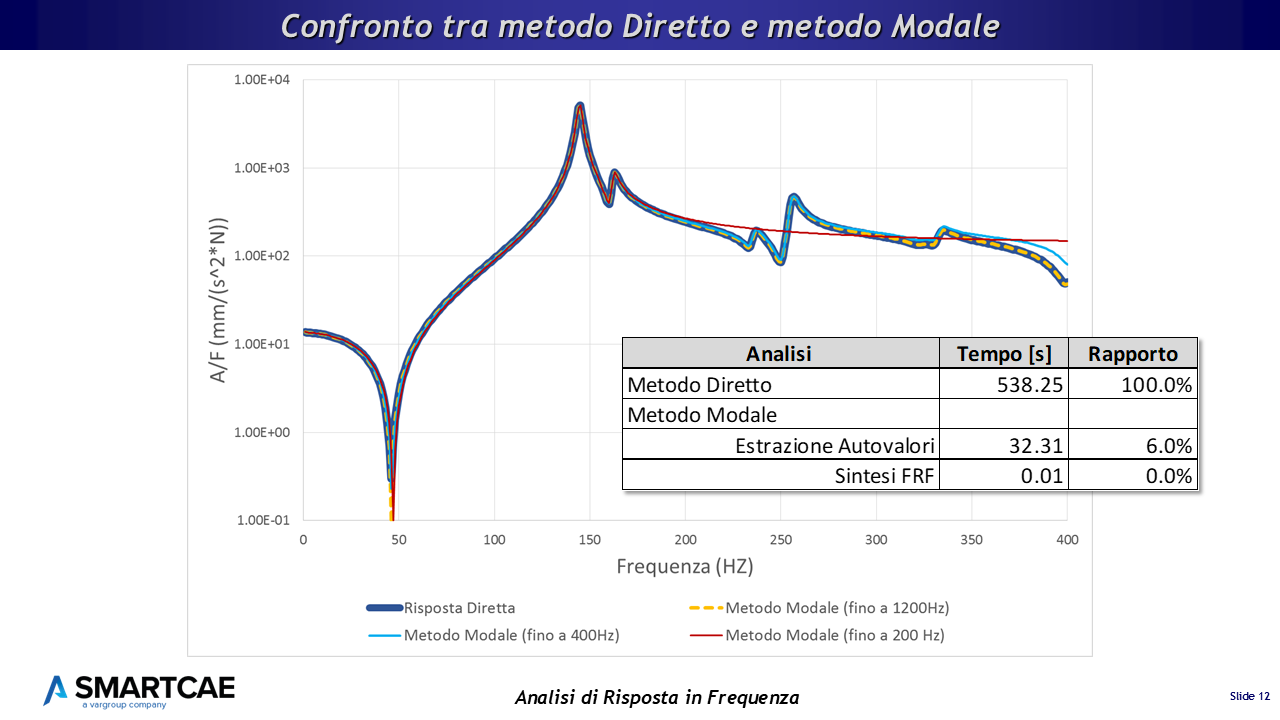
Confronto tra curve FRF calcolate con metodo diretto e metodo modale
La prima curva, quella blu scura più spessa, è la risposta calcolata con il metodo diretto e rappresenta il riferimento per questo confronto. Da un punto di vista puramente matematico, questa risposta non risente delle approssimazioni del metodo modale in quanto risolve il sistema di equazioni completo: per ciascuna frequenza (400 punti tra 1 e 400 Hz) viene ricalcolata e riassemblata la matrice del sistema e viene risolto il problema lineare. Quindi il costo computazionale corrisponde grossomodo a quello di 400 analisi statiche lineari.
La seconda curva (quella arancio tratteggiata) è quella calcolata con il metodo modale, effettuando l’estrazione degli autovalori fino a 1200 Hz, ovvero 3 volte la banda in frequenza dello studio. Si può vedere come la risposta ricalchi in maniera molto fedele quella calcolata con il metodo diretto, di fatto certificando l’accuratezza del metodo.
La terza curva, quella azzurra, mostra la risposta in frequenza calcolata con una base modale troncata alla massima frequenza di interesse, 400 Hz. Nel grafico si apprezza già a partire dai 250 HZ un leggero scostamento di questa curva prime due. Questo è dovuto al fatto che, nel computo delle FRF non entrano in gioco i modi propri della struttura oltre i 400 HZ, perché non sono stati calcolati.
Infine la curva rossa, che è palesemente errata, ovvero la sintesi dell’FRF fino a 400 Hz, ma con la base troncata a soli 200 Hz. Potete vedere che in questo caso spariscono tutti i picchi oltre i 200 Hz e come la risposta diventi piatta.
Il troncamento della base modale, rappresenta l’errore più frequente che viene commesso durante il calcolo delle curve FRF.
Da questi risultati si capisce che il metodo modale richiede che la base modale contenga un numero di autovettori adeguato, ovvero che la base sia sufficientemente estesa in una banda i frequenza sufficientemente ampia per poter replicare il comportamento dinamico con una sovrapposizione lineare delle forme modali.
Venendo agli aspetti computazionali, la tabella riporta il confronto dei tempi di calcolo del metodo diretto e di quello modale sul solito modello.
Fatto 100% il costo computazionale del metodo diretto, è evidente come l’approccio modale risulti molto meno oneroso (in questo caso circa il 6% = un ordine di grandezza in meno), occorre però fare attenzione a come viene calcolata la base modale per non incorrere nei problemi di troncamento che abbiamo appena visto.
Come si utilizzano le curve delle FRF?
Una volta che abbiamo calcolato le FRF che cosa ci facciamo?
Prendiamo il modello FEM di questo motore. Facendo l’analisi modale possiamo soltanto dire che abbiamo 13 modi tra 0 e 400 Hz, ma quale di questi può essere problematico?
Di solito si dice che i modi a frequenza più bassa hanno sono quelli da tenere d’occhio, mentre quelli a frequenze elevate sono meno problematici… ma è sempre vero?
La funzione di risposta in frequenza mi permette di esprimere in maniera sintetica il comportamento dinamico di un sistema lineare.
In pratica la curva FRF esprime la funzione di trasferimento tra il punto di applicazione del carico e il punto in cui rilevo la risposta.
Siccome in un sistema lineare la risposta è indipendente dall’intensità del carico applicato, la curva FRF mi permette di identificare rapidamente le zone in cui una forzante armonica potrebbe accoppiarsi con una risonanza del modello, indicando di quanto viene amplificata la risposta. In altre parole, vediamo un picco nel grafico al quale è associato un valore di frequenza e un ampiezza. Da queste riusciamo rapidamente a capire se abbiamo un problema di risonanza o meno.
Ad esempio in questo caso vediamo che esiste un picco in direzione Y corrispondente alla prima frequenza di risonanza di 144 Hz.
Invece in direzione Z è presente un picco più alto, intorno ai 336 Hz. Pertanto il comportamento dinamico alle frequenze più elevate può richiedere delle modifiche al progetto per limitare questa risposta. A questo punto potrei andare a vedere la forma dei modi a 336Hz per capire come di deforma il sistema, e studiare un modo per modificarne la flessibilità.
Progettualmente si può poi intervenire per modificare la risposta con vari metodi:
- Introdurre irrigidimenti locali e globali per spostare verso frequenze più alte la risonanza che crea problemi.
- Introdurre delle zavorre o della cedevolezza per spostare verso frequenze più basse la risonanza che crea problemi.
- Inserire componenti quali ammortizzatori che con il loro smorzamento possono abbattere l’ampiezza della risposta.
- Inserire dei silent block per disaccoppiare elasticamente due componenti e dissipare localmente l’energia che passa per il giunto.
- Studiare un assorbitore tarato (in gergo tuned absorber) che si accoppi con la risonanza incriminata, si tratta di aggiungere un nuovo grado di libertà al sistema la cui risonanza locale ha la capacità di modificare la frequenza del modo globale che voglio spostare.
Riepilogo
Riassumendo rapidamente quello che abbiamo visto in questo post.
Per un sistema lineare elastico è possibile definire una grandezza, che prende il nome di Funzione di Risposta in Frequenza che rappresenta la funzione di trasferimento tra il punto di applicazione di una forzante armonica e il punto in cui vado a rilevare la risposta. L’FRF è normalizzata rispetto alla forzante e quindi non dipende dall’intensità del carico.
La risposta in frequenza dipende, oltre che dalla distribuzione di massa e rigidezza, anche dallo smorzamento. Esistono vari tipi di smorzamento e varie maniere per schematizzarlo all’interno di un modello FEM, abbiamo visto lo smorzamento Viscoso, quello Strutturale e quello Modale.
Abbiamo visto due modi numerici per il calcolo della FRF:
- il metodo diretto, che prevede la risoluzione di un problema statico lineare per ogni passo in frequenza della risposta che voglio calcolare (metodo lento ma accurato)
- il metodo modale, che si basa sulla trasformazione delle equazioni del problema nello spazio vettoriale costituito dagli autovalori del modello (metodo più rapido computazionalmente, ma che può essere soggetto agli errori di troncamento).
Infine abbiamo visto come interpretare i risultati delle curve FRF. In particolare l’analisi modale e le FRF sono sono intimamente legate, essendo entrambi due diverse rappresentazioni della dinamica del medesimo modello. L’utilizzo sinergico di entrambi può aiutare a comprendere il comportamento del prodotto e prevenire e risolvere eventuali problemi legati alle vibrazioni.
Domande e Risposte
Nel seguito sono indicate alcune domande che mi sono state sottoposte nel corso di seminari e webinar dedicati all’analisi di risposta in frequenza con gli elementi finiti. Ho deciso di riportarle in questo post perché potranno esserti di aiuto nel definire la migliore strategia di modellazione FEM per le tue analisi dinamiche.
Quale tipo di smorzamento mi conviene utilizzare per l’analisi FRF?
Dipende molto dal tipo di metodo che utilizzo per la sintesi della funzione di risposta in frequenza.
Se si utilizza l’approccio modale, lo smorzamento modale è quello più immediato, ma si tratta di un attributo «globale» sul modo, che coinvolge il movimento di tutta la struttura e che lascia disaccoppiate le equazioni modali.
Viceversa sia nel metodo diretto che nel metodo modale, è possibile utilizzare lo smorzamento viscoso e quello strutturale, potendo differenziare lo smorzamento tra materiali e componenti diversi.
Posso modellare uno smorzatore concentrato utilizzando il metodo modale?
La risposta è si, è possibile modellare un damper concentrato che collega due punti del modello anche con il metodo modale.
La matrice di smorzamento dell’elemento viene trasformata nello spazio modale e rendere accoppiate le equazioni modali.
C’è da tenere presente che lo smorzamento concentrato si somma al valore dello smorzamento modale e si corre il rischio di sovrastimare l’effettivo smorzamento del sistema.
Quando si pensa di dover gestire uno smorzamento concentrato molto alto, un suggerimento è quello di eseguire le varie iterazioni di progetto utilizzando l’approccio modale, ma alla fine di ripetere il calcolo con il metodo diretto per verificare di non aver commesso errori nella stima dello smorzamento.
Nella figura “slide 12” c’è un picco negativo intorno a 50HZ: cosa rappresenta? che significato fisico ha?
Quella porzione di curva prende il nome di anti-risonanza. E’ l’opposto della risonanza. Alla risonanza basta una forzante molto piccola per generare ampie oscillazioni, si ha un’amplificazione.
All’anti-risonanza, in questo caso specifico quando eccito nell’intorno dei 50Hz, questo punto non manifesta oscillazioni e la funzione di trasferimento va a zero.
Per esperienza, lo smorzamento dei giunti varia con la frequenza di eccitazione? Come posso fare a modellarlo?
Se, come capisco, si sta parlando dello smorzamento di giunzioni, quindi zone limitate della struttura, con NASTRAN è possibile utilizzare gli elementi BUSH, che sono elementi di collegamento punto a punto, che permettono di definire 6 valori di rigidezza e 6 valori di smorzamento, uno per ciascun grado di libertà.
Questo valore può fare riferimento a una funzione nella quale è possibile esprimere come tabella il valore della rigidezza e dello smorzamento al variare della frequenza.
È possibile utilizzare elementi gap con l’analisi di risposta in frequenza?
La risposta è NO. Non è possibile utilizzare gli elementi GAP nella risposta in frequenza, così come non è possibile utilizzarli nell’analisi modale.
Questi tipi di analisi presuppongono la linearità del sistema, pertanto un elemento non lineare come il GAP, o come le superfici di contatto, non può essere utilizzato.
Per schematizzare i collegamenti dovrò quindi utilizzare collegamenti lineari, quali l’incollaggio, gli elementi BUSH, o gli RBE.
Argomenti collegati
Articoli
- Cosa è l’analisi modale con gli elementi finiti
- Cosa è l’analisi transitoria con gli elementi finiti
Webinar