Indice dei contenuti
In questo articolo spieghiamo come funzionano le analisi transitorie e quali risultati forniscono per la verifica dei progetti.
I problemi della dinamica strutturale possono essere divisi in due categorie principali. In una l’obiettivo è quello di determinare il comportamento in frequenza della struttura e calcolare, ad esempio le frequenze di vibrazione e le corrispondenti forme modali. Nell’altra l’obiettivo è quello di determinare come la struttura si comporta nel tempo durante l’applicazione di un carico.
Nei primi due articoli di questa serie abbiamo parlato dell’analisi modale e della risposta in frequenza.
In questo articolo ci concentriamo sull’analisi transitoria.
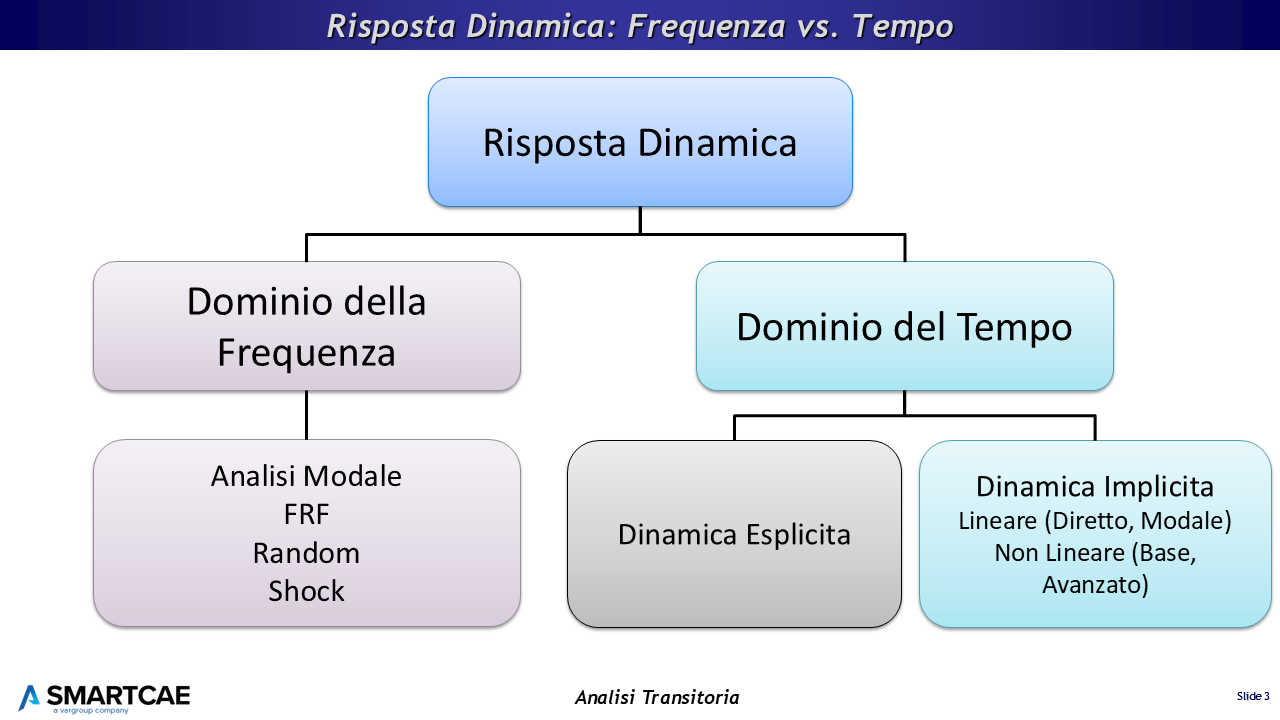
Tipi di analisi dinamiche che è possibile eseguire con gli elementi finiti.
Analisi Transitoria
A differenza delle analisi statiche e delle analisi in frequenza, nell’analisi transitoria le forze variano in funzione del tempo con una legge qualsiasi, non necessariamente con una legge di tipo sinusoidale come nelle ipotesi delle risposte in frequenza.
I carichi possono essere sia forze ma anche spostamenti imposti con una legge temporale qualsiasi.
Per l’analisi dinamica transitoria esistono due marco categorie di solutori, che prendono il nome dal tipo di tecnica numerica utilizzata:
- I metodi Espliciti. Sono stati sviluppati per risolvere brevi storie temporali con fortissime non linearità. Come ad esempio vedere cosa succede ad una struttura nel corso di una esplosione, oppure la simulazione di un crash automobilistco, oppure una prova di impatto balistico.
- I metodi Impliciti. Sono quelli utilizzati con maggiore frequenza per gestire storie temporali lunghe, con fenomeni non lineari limitati o nulli. Questo è il tema del seminario di oggi.
Per quanto riguarda la gestione del problema, nell’ipotesi di sistema lineare NX Nastran offre due tecniche numeriche per gestire l’analisi transitoria: il metodo diretto e il metodo modale, che cominceremo a conoscere già dalla prossima slide. Sostanzialmente, come abbiamo visto nel seminario sulla risposta in frequenza, il metodo diretto risolve le equazioni complete del sistema, mentre il metodo modale utilizza una trasformazione di coordinate per disaccoppiare le equazioni del problema.
Se l’ipotesi di linearità non è applicabile, è possibile eseguire una simulazione transitoria non-lineare. Anche in questo caso abbiamo due opzioni: il solutore Base e il Non Lineare Avanzato.
Analisi transitoria diretta: lineare e non lineare

Analisi transitoria diretta – lineare e non lineare
Riprendiamo l’equazione del moto di un sistema elastico, nel quale appaiono le forze di inerzia, di attrito viscoso, elastiche, che istantaneamente devono essere in equilibrio con le forze applicate. Facciamo l’ipotesi di sistema lineare.
Nell’analisi strutturale transitoria diretta la risposta è calcolata risolvendo questo sistema di equazioni utilizzando una integrazione numerica diretta. Il metodo numerico utilizzato è lo stesso per l’analisi transitoria diretta Lineare e Non Lineare e consente la gestione di time-step adattativi (ovvero che possono essere contratti o dilatati alla bisogna da solutore per aiutare la convergenza).
Attraverso l’integrazione numerica diretta, l’equilibrio è soddisfatto per istanti temporali discreti di intervallo DeltaT.
L’evoluzione delle variabili nel tempo è calcolata con l’algoritmo di Newmark-Beta, che appartiene alla famiglia dei metodi alle differenze finite. Conoscendo la configurazione del sistema all’istante iniziale, questo metodo permette di ricavare la soluzione all’istante temporale successivo. Tale soluzione diviene poi la condizione iniziale per il successivo step di calcolo e il calcolo prosegue.
La differenza sostanziale tra l’analisi transitoria lineare e quella non lineare è che la prima presuppone la linearità del sistema (e quindi si limita all’integrazione temporale), mentre la seconda permette di considerare effetti non lineari come grandi spostamenti, comportamento di materiale non lineare, contatto. La convergenza non lineare è raggiunta ad ogni time step utilizzando il medesimo metodo Newton-Raphson iterativo che viene utilizzato nell’analisi statica non-lineare.
Qui sono riportati i codici delle soluzioni transitorie dirette: la SOL 109 per problemi lineari, la SOL 129 per i problemi non-lineari, la SOL 601 per l’utilizzo del solutore non-lineare avanzato.
Analisi transitoria con metodo modale
In questa slide provo a riassumere a grandi linee l’approccio modale.
Nell’ipotesi di linearità del sistema, è possibile trasformare le equazioni del sistema cambiando la base. In particolare si utilizza lo spazio vettoriale costituito dagli autovettori del sistema. Vi rimando al seminario sull’analisi modale e quello sulla risposta in frequenza per un approfondimento.

Analisi transitoria con metodo modale
Per farla molto breve, sostituendo la variabile U con [csi], e pre-moltiplicando tutti i termini per la matrice trasposta della base si riesce a disaccoppiare il sistema di equazioni, riducendo anche il numero di equazioni, pari alle coordinate modali che abbiamo selezionato.
Inoltre, nell’ipotesi di smorzamento viscoso, è possibile riscrivere l’equazione in questa maniera.
A questo punto l’integrazione temporale avviene con l’algoritmo di Newmark-Beta, ma con un costo computazionale decisamente inferiore rispetto al modello di partenza.
Una volta trovate le incognite [csi_i] per ogni istante temporale, le coordinate modali vengono ri-proiettate nello spazio euclideo attraverso un semplice prodotto riga per colonna. Dagli spostamenti vengono poi calcolati gli stress e gli altri risultati.
Questa procedura è quella che viene effettuata nella SOL 112 di Nastran.
In maniera analoga a quanto avviene nell’analisi di risposta in frequenza, i risultati sono fortemente condizionati dalla scelta degli autovettori. Una base modale inadeguata potrebbe non essere in grado di rappresentare correttamente il comportamento transitorio.
Se la nostra base modale è troncata ad una certa frequenza, il modello non sarà in grado di rappresentare le oscillazioni di frequenza più alta.
Come introdurre lo smorzamento nell’analisi transitoria
Anche con la risposta transitoria, abbiamo a che fare con lo smorzamento.
Come abbiamo visto nell’articolo dedicato alla risposta in frequenza esistono due tipi di smorzamento, quello strutturale che dipende dagli spostamenti, e quello viscoso che dipende dalla velocità.

Come introdurre lo smorzamento nell’analisi transitoria
Lo smorzamento strutturale ha la caratteristica di rendere complessa la matrice di rigidezza, cosa che non è fattibile per la risposta nel tempo, pertanto i solutori FEM usano un trucco per trasformare lo smorzamento strutturale in uno smorzamento viscoso equivalente.
Dal grafico si vede che al variare della frequenza di oscillazione, questi due smorzamenti sono identici soltanto per una frequenza particolare, quando si incrociano le due curve.
Per questa frequenza lo smorzamento strutturale può essere modellato utilizzando uno smorzamento viscoso equivalente, che è quello che fa Nastran per evitare di dover gestire matrici complesse.
Dall’equazione si vede come ragiona Nastran per la creazione della matrice di smorzamento del modello.
- Per prima cosa si prendono gli smorzamenti viscosi concentrati nel modello matrice [Bdamp].
- A questi si possono sommare due termini:
- Con il PARAM, G definisco un coefficiente di smorzamento strutturale che va a moltiplicare la matrice assemblata di rigidezza. Questo smorzamento viene diviso per il valore della pulsazione definita con PARAM, W3. Il default questo valore è zero e il termine non viene aggiunto.
- Con il PARAM, W4 trasformo lo smorzamento strutturale degli elementi per i cui materiali è stato definito lo smorzamento. Anche in questo caso se non definisco il valore di W4, questo termine non viene aggiunto.
Tramite l’approccio modale è possibile definire un coefficiente di smorzamento che dipende dalla frequenza di oscillazione e che non ha una corrispondenza diretta con le proprietà degli elementi. Bisogna stare attenti a non introdurre due volte lo smorzamento (quello degli elementi e quello modale).
Esempio di analisi transitoria non lineare
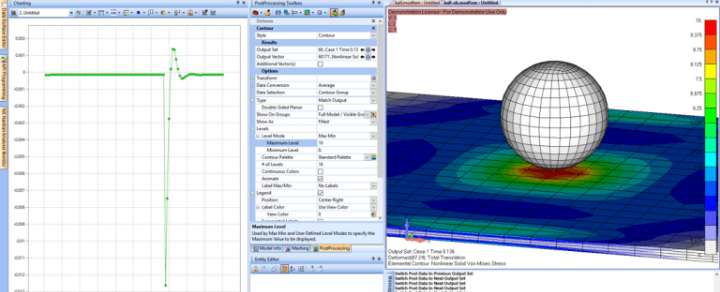
Nell’immagine è riportato un esempio di analisi non lineare transitoria eseguita con il solutore non lineare avanzato di NX Nastran per simulare il transitorio di una palla che rimbalza su un piano.
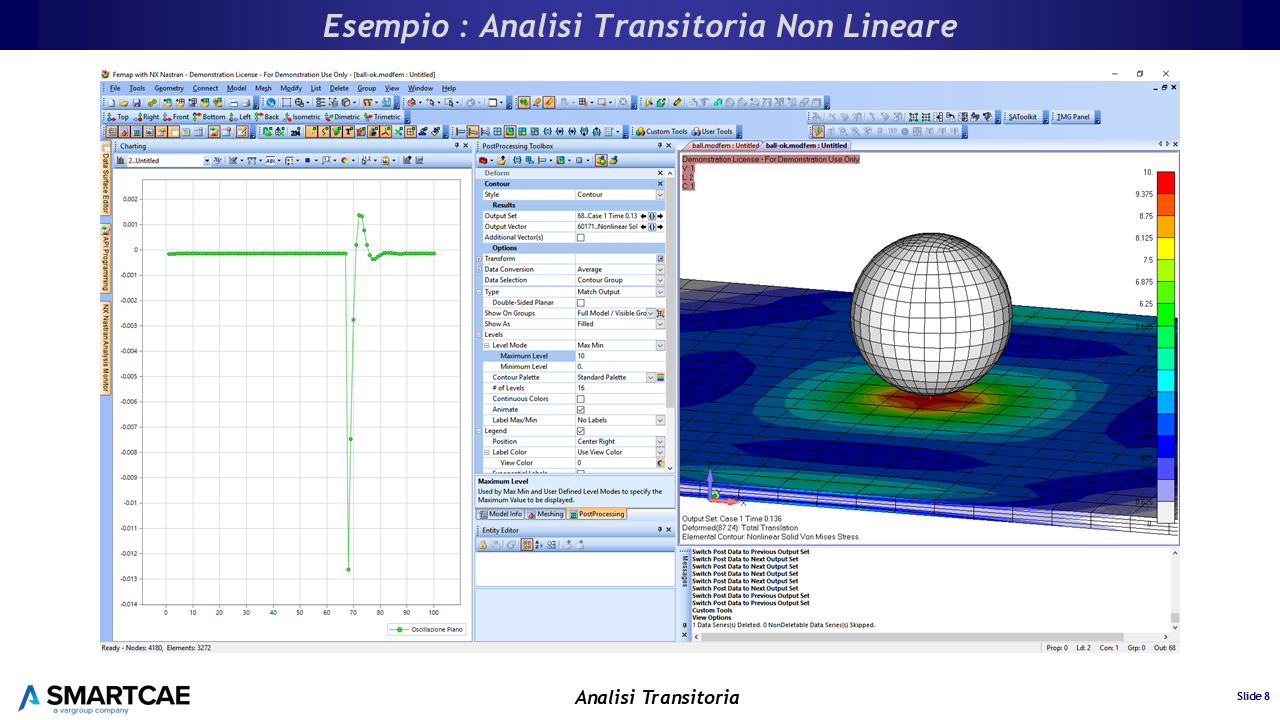
Esempio di analisi transitoria non lineare con Femap e NX Nastran
Nel modello sono considerati sia i grandi spostamenti che il contatto 3D superficie-superficie.
Puoi vedere il filmato della simulazione e maggiori informazioni su questo modello guardando la registrazione del webinar sull’analisi transitoria FEM.
Riepilogo
L’analisi transitoria permette di determinare il comportamento della struttura soggetta a carichi variabili nel tempo che non necessariamente possono essere ricondotti a uno spettro di eccitazione sinusoidale in frequenza.
Abbiamo scoperto che esistono più modi per impostare un’analisi transitoria:
- Se ho a che fare con sistemi nei quali è valida l’ipotesi di linearità, ho la possibilità di scegliere se utilizzare l’approccio diretto, ovvero risolvere le equazioni di Newton sul sistema completo, oppure utilizzare l’approccio modale. Questi due approcci, se impostati correttamente, portano al solito risultato.
- In generale il metodo modale è da preferire quando ho un modello con tanti gradi di libertà, ma il contenuto armonico della forzante e della risposta è limitato, quindi con pochi autovettori riesco a calcolare la risposta del sistema.
- Al contrario quando il contenuto in frequenza è elevato (quindi dovrei calcolare tanti autovettori) oppure devo considerare correttamente lo smorzamento del sistema e non posso approssimarlo con uno smorzamento viscoso equivalente (es. ho un elevato smorzamento strutturale) è da preferire il metodo diretto.
- Se nel modello sono presenti aspetti non lineari come materiali non lineari, grandi spostamenti o contatti, devo per forza di cose utilizzare la soluzione non lineare transitoria. Anche in questo caso con NX Nastran ho la possibilità di utilizzare il solutore non-lineare transitorio base (la SOL 129) oppure utilizzare il solutore Non Lineare Avanzato (SOL 601). Una discriminante importante nella scelta dell’approccio da utilizzare dipende essenzialmente se nel modello sono presenti dei contatti e che tipo di elemento voglio utilizzare per schematizzarlo. Con la SOL129 posso utilizzare soltanto elementi GAP e Slide Line, mentre con la SOL 601 ho a disposizione il contatto superficie-superficie, quindi più adatto a geometrie 3D.
Domande e risposte
Ecco alcune domande che mi sono state sottoposte nel corso di seminari e webinar dedicati alla modellazione FEM di fenomeni transitori. Ho deciso di riportarle in questo post perché potranno esserti di aiuto nel definire la migliore strategia di modellazione per le tue analisi FEM.
Con NX Nastran è possibile anche effettuare simulazioni dinamiche esplicite?
Anche se per brevità in questo seminario abbiamo parlato soltanto delle simulazioni FEM transitorie implicite, le confermo che con il solutore Non Lineare avanzato di NX Nastran è possibile eseguire simulazioni transitorie esplicite. Il codice della soluzione è SOL 701.
In futuro probabilmente parleremo nel dettaglio di questo tipo di simulazione.
E’ possibile simulare fenomeni con forzanti transitorie diverse che agiscono su più punti?
Si, non c’è un limite particolare sul numero di forzanti applicabili.
Nell’analisi transitoria posso applicare sia forze puntuali, che spostamenti imposti.
Questi non necessariamente devono essere sincronizzati.
Posso anche eseguire una storia temporale in cui un carico si attiva e poi si disattiva nel corso della storia temporale.
Può rispiegare quali sono i vantaggi del metodo modale rispetto al metodo diretto e viceversa?
Cominciamo con il metodo diretto.
Il metodo diretto risolve le equazioni complete del moto del sistema, tenendo conto di inerzia, smorzamento e elasticità, bilanciandole con le forze. Le forze hanno due contributi: le forze applicare e le forze dovute alle non-linearità. Per questo motivo il metodo diretto permette di gestire transitori non-lineari. Lo svantaggio del metodo diretto è legato ai tempi di calcolo che dipendono dal numero di gradi di libertà del modello.
Il metodo modale esegue la trasformazione delle coordinate nello spazio utilizzando come base gli autovettori del modello. Questo è possibile soltanto ipotizzando la linearità del sistema, pertanto l’approccio modale non può tenere conto delle non-linearità. Il vantaggio è quello di disaccoppiare le equazioni del modello e, tendenzialmente, di avere un numero di gradi di libertà inferiore di svariati ordini di grandezza rispetto al modello di partenza, con tempi di calcolo ridotti.
Siccome è richiesta l’estrazione delle forme modali, se devo considerare un contributo armonico elevato, potrei essere costretto a calcolare centinaia o migliaia di forme modali, in quanto la densità modale aumenta col crescere della frequenza. Pertanto si perdono i vantaggi del metodo modale rispetto a quello diretto.
La scelta del time-step è critica anche per analisi implicite come per lo è anche per le analisi esplicite?
In una simulazione transitoria implicita la scelta del time-step è meno critica rispetto alla simulazione esplicita. In particolare il time-step non dipende dalle dimensioni della mesh.
Analogamente a quanto si fa per l’analisi modale, per rappresentare correttamente una oscillazione occorre prendere almeno 4-5 punti nella semionda, ovvero 8-10 punti sull’onda.
Questo vuol dire che se voglio catturare l’animazione di una oscillazione con frequenza F, ovvero con periodo T=1/F, ho bisogno di avere un time step che sia almeno 1/8 o 1/10 rispetto a questo periodo.
Tenete comunque presente che l’analisi transitoria è stabile anche se definisco un time step più grande, l’inconveniente è quello di non riuscire a catturare le oscillazioni a frequenza elevata e potenzialmente incorrere in problemi di aliasing temporale.
Argomenti collegati
Articoli
- Cosa è l’analisi modale con gli elementi finiti
- Cosa è l’analisi di risposta in frequenza con gli elementi finiti
Webinar